Trie
Trie란 Prefix Tree나 Radix Tree라고도 불리는 트리 형태의 자료구조로, reTRIEval 에서 유래한 이름을 가지고 있다.
Trie는 각 노드가 string으로 된 key를 나타내고, 각 엣지 (간선)가 하나의 알파벳을 나타내는 트리 형태의 자료구조로, key-value 쌍을 저장하도록 하면 map처럼 associative array로 이용할 수 있고, 그냥 key만 저장하면 어떤 string이 집합에 속하는지 확인하기 위한 set처럼 삽입/삭제가 가능한 집합 자료구조로 이용할 수 있다.
흔히 사용되는 std::map/std::set의 내부 구현인 Red-black tree (balanced binary search tree/self-balancing binary search tree)와 비교해보면 각 연산 (검색, 삽입)이 다음과 같은 시간 복잡도를 갖는다 ($L$: key로 이용되는 문자열의 최대 길이, $N$: key의 개수, 즉 자료구조의 원소 개수):
| 연산 | BBST | Trie |
|---|---|---|
| 삽입 | $O(L\mathrm{log}N)$ | $O(L)$ |
| 검색 | $O(L\mathrm{log}N)$ | $O(L)$ |
{"AA", "AC", "BC", "BCG", "C", "CC"} 의 문자열을 원소로 갖는 Trie를 그림으로 나타내면 다음과 같다:
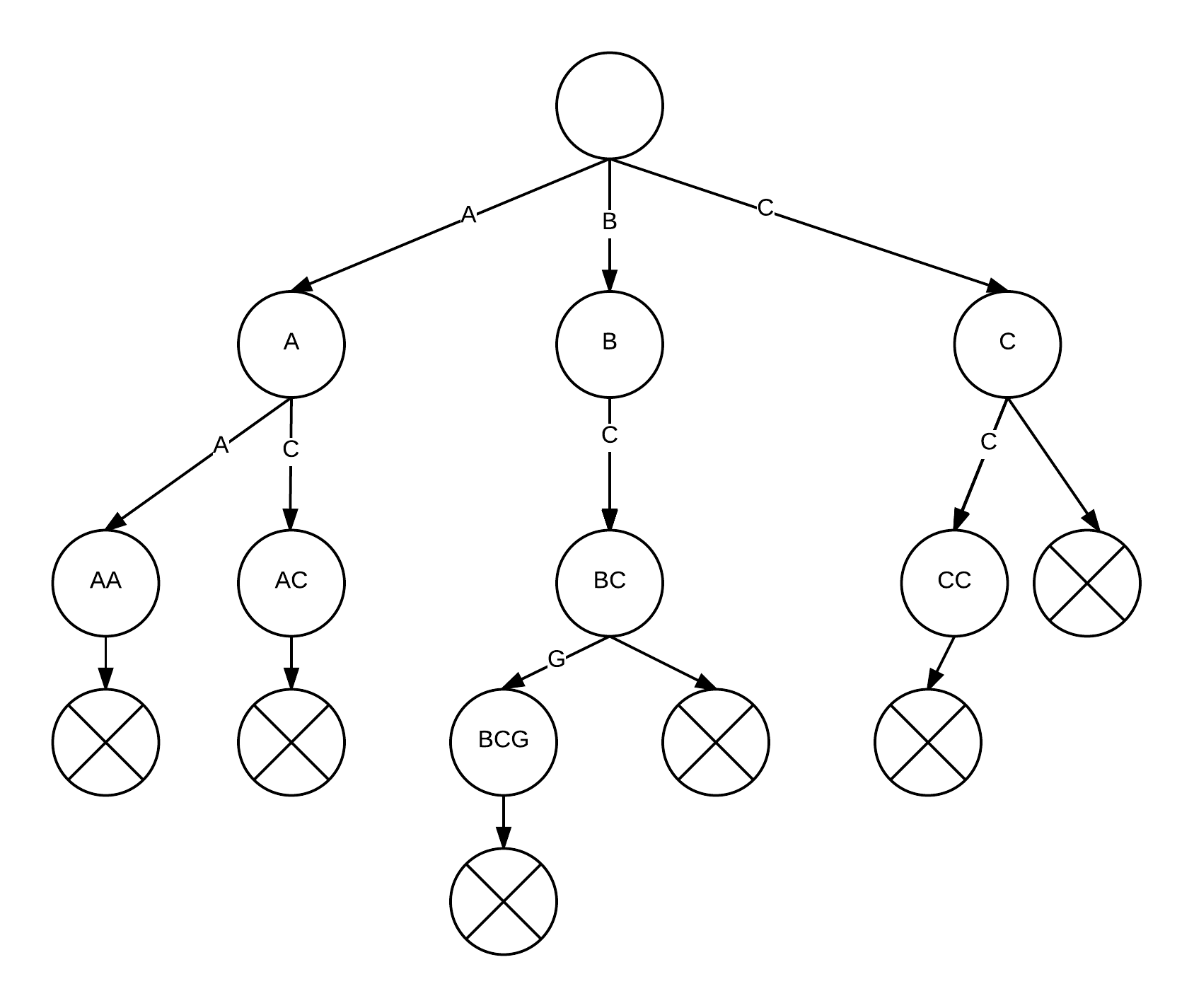
$\otimes$로 표현되는 노드는 해당 노드로 끝나는 문자열이 존재한다는 의미인데, 예를 들어 이 집합에 "A"는 존재하지 않지만 "AA"는 존재하므로 "AA"를 나타내는 노드에서는 $\otimes$로 표현되는 노드로의 간선이 존재하지만 "A"를 나타내는 노드에서는 간선이 존재하지 않는 것을 확인할 수 있다. (이후 $\otimes$ 로 나타나는 노드로 연결되는 간선을 "$"로 표현)
연산의 경우 BST처럼 삽입 과정이 검색과 굉장히 닮아있기 때문에, 검색부터 살펴보도록 하자.
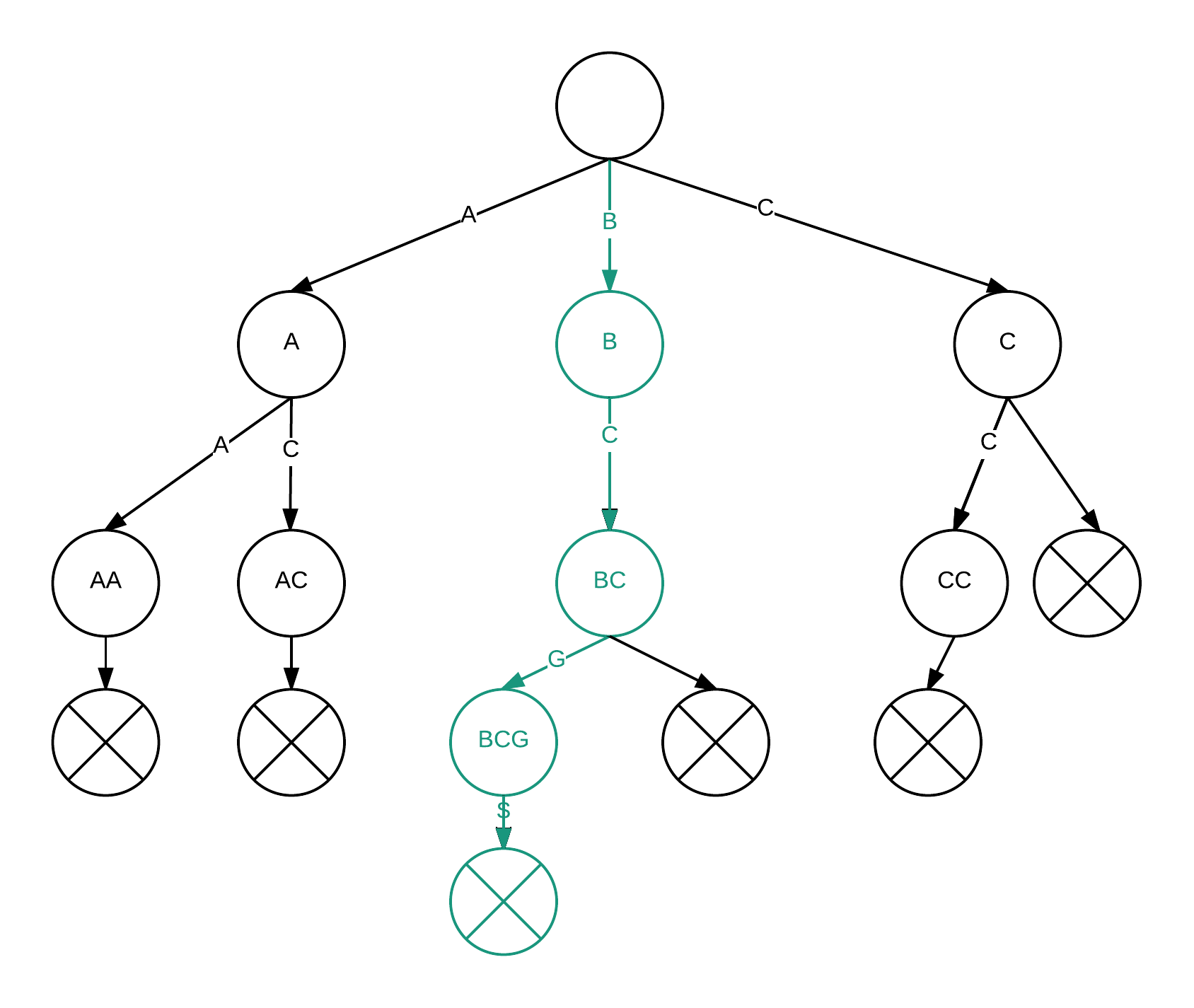
"BCG"를 검색하는 경우
루트에서 시작해서, 해당 알파벳을 나타내는 간선을 따라 쭉쭉 따라가면 끝. 단, "BGC"를 "BCG$"로 고려해야 한다. 만약 중간에 NULL을 만나게 된다면 (존재하지 않는 간선을 선택하게 된다면) 해당 문자열은 집합에 존재하지 않는다는 결론이 나오고, 그렇지 않을 경우 해당 문자열이 집합에 존재한다는 것을 확인할 수 있다.
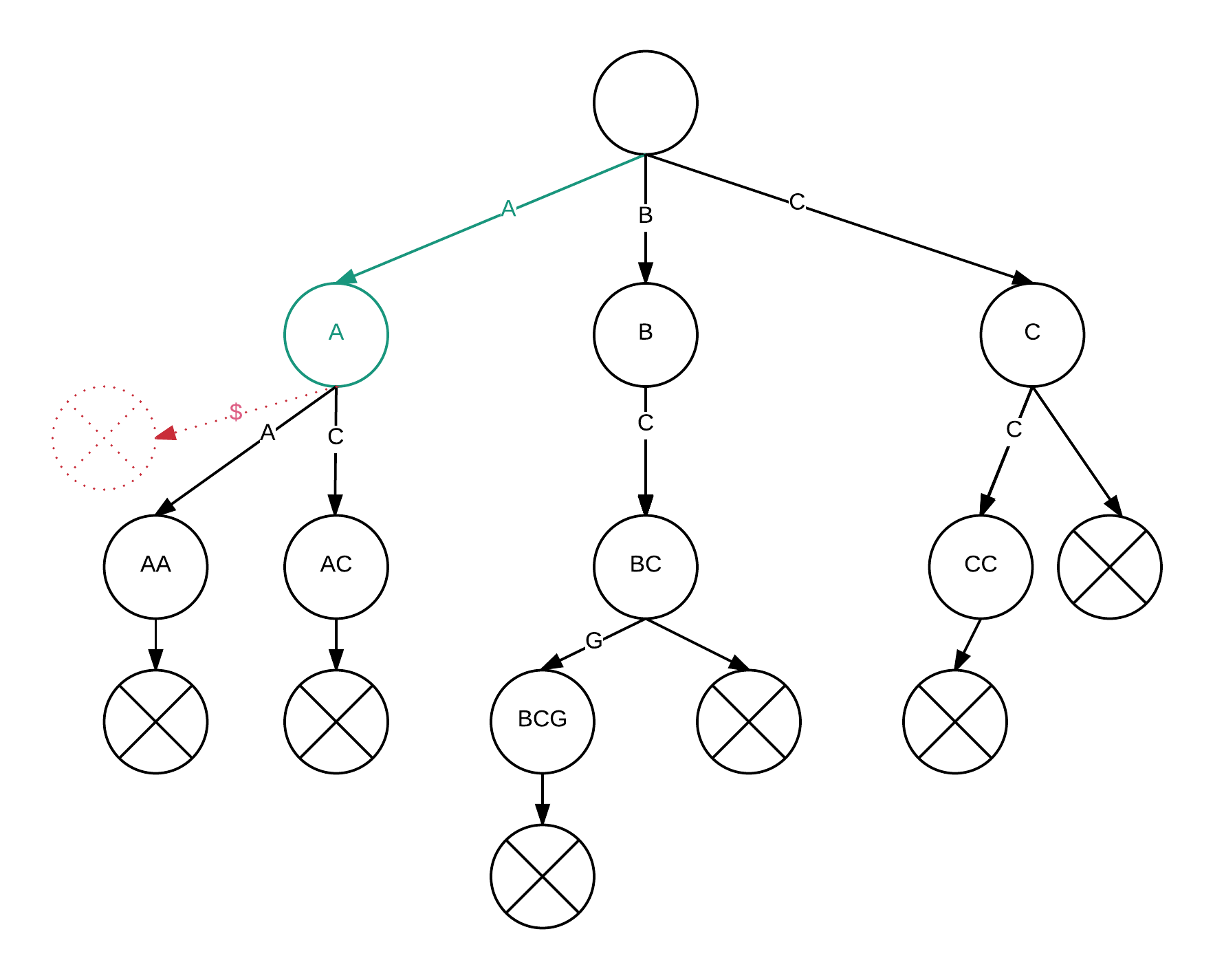
"A"를 검색하는 경우
마찬가지로 "A$"를 생각하면, 중간에 $을 나타내는 간선이 존재하지 않아 실패하는 것을 볼 수 있다.
삽입
검색을 보면서 깨달았겠지만, 삽입은 검색을 하는 도중 실패한 부분부터 간선을 추가해나가는 식으로 반복하면 간단!
삭제
삭제 역시도 각 노드에 rereference count 를 관리하면서 0이 되는 순간 노드와 간선을 지워주는 형태로 구현하면 간단하다.